計(jì)算塑料的抗彎強(qiáng)度通常通過彎曲測(cè)試來完成，特別是三點(diǎn)彎曲或四點(diǎn)彎曲測(cè)試。這里我們以四點(diǎn)彎曲測(cè)試為例說明如何計(jì)算塑料的抗彎強(qiáng)度。
四點(diǎn)彎曲測(cè)試中抗彎強(qiáng)度的計(jì)算
對(duì)于四點(diǎn)彎曲測(cè)試，假設(shè)加載點(diǎn)位于兩個(gè)支撐點(diǎn)之間，并且這兩個(gè)加載點(diǎn)等距分布，則最大彎矩發(fā)生在兩加載點(diǎn)之間的中心位置。此時(shí)，可以使用以下公式計(jì)算抗彎強(qiáng)度：
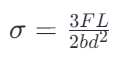
其中：
表示抗彎強(qiáng)度（單位：帕斯卡 Pa 或兆帕 MPa）
是導(dǎo)致試樣斷裂的最大載荷（單位：牛頓 N）
是支撐點(diǎn)之間的距離（即跨度，單位：米 m）。注意，在四點(diǎn)彎曲的情況下，這指的是兩個(gè)外側(cè)支撐點(diǎn)之間的距離。
是試樣的寬度（單位：米 m）
是試樣的厚度（單位：米 m）
注意事項(xiàng)
單位轉(zhuǎn)換：確保所有尺寸都轉(zhuǎn)換為國(guó)際單位制（SI單位），尤其是力以牛頓(N)，長(zhǎng)度以米(m)表示。如果原始數(shù)據(jù)不是以這些單位給出的，請(qǐng)先進(jìn)行單位轉(zhuǎn)換。
加載模式：上述公式適用于內(nèi)距加載的情況，即兩個(gè)加載點(diǎn)位于兩個(gè)支撐點(diǎn)內(nèi)部且等距分布。如果是其他加載配置，計(jì)算公式可能會(huì)有所不同。
遵循標(biāo)準(zhǔn)：根據(jù)所使用的具體材料類型，可能需要參考特定的標(biāo)準(zhǔn)指南進(jìn)行測(cè)試和計(jì)算，例如ASTM D790（塑料的彎曲屬性）、ISO 178（塑料的彎曲性能）等。這些標(biāo)準(zhǔn)會(huì)提供詳細(xì)的測(cè)試程序、推薦的試樣尺寸以及具體的計(jì)算方法。
三點(diǎn)彎曲測(cè)試中的抗彎強(qiáng)度計(jì)算
在三點(diǎn)彎曲測(cè)試中，抗彎強(qiáng)度的計(jì)算公式略有不同：
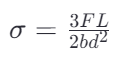
這里的 是在三點(diǎn)彎曲情況下施加的中心載荷， 是支撐點(diǎn)之間的距離（即跨度），其余變量含義相同。
總結(jié)
無論是采用三點(diǎn)還是四點(diǎn)彎曲測(cè)試，計(jì)算塑料的抗彎強(qiáng)度都需要準(zhǔn)確測(cè)量施加的載荷、試樣的幾何尺寸，并根據(jù)相應(yīng)的公式進(jìn)行計(jì)算。此外，遵循相關(guān)的國(guó)際或行業(yè)標(biāo)準(zhǔn)能夠確保測(cè)試結(jié)果的有效性和可重復(fù)性。正確地應(yīng)用這些方法可以幫助評(píng)估塑料材料在受彎條件下的性能，這對(duì)于工程設(shè)計(jì)和材料選擇至關(guān)重要。
下一篇：維氏硬度測(cè)試方法具體介紹
- 化妝品常用的包裝標(biāo)識(shí)含義詳情
- GB/T 2423.22-2012溫度變化試驗(yàn)：揭示產(chǎn)品缺陷的關(guān)鍵環(huán)境應(yīng)力篩選
- 防腐等級(jí)C4/C5解讀：工業(yè)環(huán)境選材的關(guān)鍵依據(jù)
- GJB 360B-2009 解讀：電子及電氣元件試驗(yàn)方法標(biāo)準(zhǔn)詳解
- 相機(jī)可靠性測(cè)試全解析：從實(shí)驗(yàn)室到戶外的20項(xiàng)關(guān)鍵驗(yàn)證
- 材料臭氧老化腐蝕試驗(yàn)：守護(hù)材料耐用性的關(guān)鍵防線
- 詳解第三方檢測(cè)機(jī)構(gòu)的作用與核心優(yōu)勢(shì)
- 二氧化氮?dú)怏w腐蝕試驗(yàn)：評(píng)估材料在嚴(yán)酷環(huán)境下的耐久性與性能
- MTBF與MTTR解析：理解設(shè)備可靠性與維護(hù)效率的關(guān)鍵指標(biāo)
- 汽車電子耐候性試驗(yàn)解析：保障車載電子設(shè)備環(huán)境適應(yīng)性與可靠性的關(guān)鍵流程